M5 V Flächeninhalt: Unterschied zwischen den Versionen
Aus RMG-Wiki
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 33: | Zeile 33: | ||
{{Box| Übung zur Umwandlung bei gemischten Einheiten| | {{Box| Übung zur Umwandlung bei gemischten Einheiten| | ||
Bei den Aufgaben steht im blauen Kästchen ein Beispiel, wie die Lösung in deinem Heft aussehen soll. | Bei den Aufgaben steht im blauen Kästchen ein Beispiel, wie die Lösung in deinem Heft aussehen soll. | ||
* Bearbeite im Buch S.228/2a,c, | * Bearbeite im Buch S.228/2a,c,i-k und 3a,c,e-g | ||
* Jetzt kommen Kommas hinzu. Wenn du dir unsicher bist, so lies oben auf Seite 228 die Information zur Kommaschreibweise durch. | * Jetzt kommen Kommas hinzu. Wenn du dir unsicher bist, so lies oben auf Seite 228 die Information zur Kommaschreibweise durch. | ||
* Bearbeite S.228/5 a-h und 7 e-i | * Bearbeite S.228/5 a-h und 7 e-i | ||
Version vom 9. Juli 2020, 11:29 Uhr
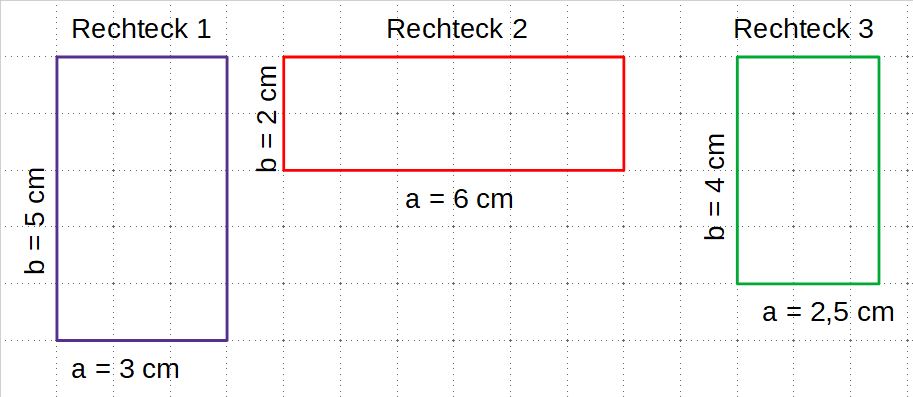
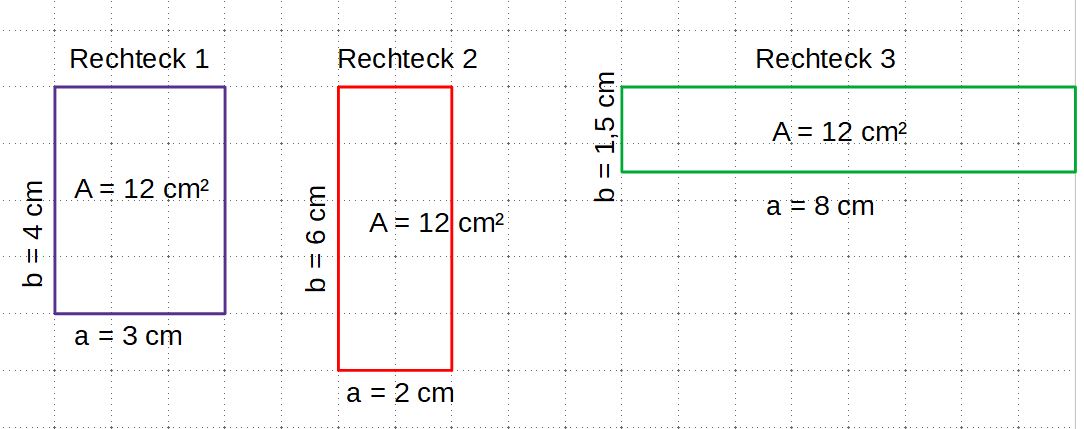
1 Flächenvergleich
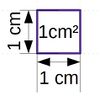
2 Einheiten für Flächeninhalte
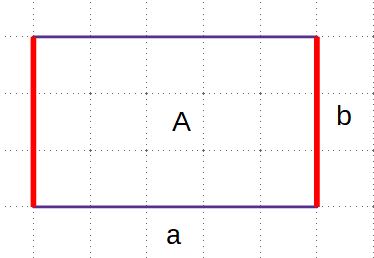
Flächeninhalt und Umfang von Rechtecken
a) A=4cm*7cm= 28cm²; U = 2*4cm + 2*7cm = 22cm
b) A = 4mm*7mm = 28 mm²; U = 2*4mm + 2*7mm = 22mm
c) A = 5dm*12dm = 60 dm²; U = 2*5dm + 2*12dm = 34cm
Falls ihr mit anderen Einheiten gerechnet habt, dann vergleicht die Lösungen am Ende. Dort sind sie in verschiedenen Einheiten angegeben.
a) A= 5cm*70dm= 5cm*7cm= 35cm² = 3500dm²
b) A = 1200mm*9dm = 12dm*9dm = 108dm² = 10800cm² = 1080000mm²
c) A = 5km*3000m = 5km*3km = 15 km² = 1500 ha = 150 000a = 15 000 000 m²
d) A = 50cm*200mm = 50cm*20cm = 1000 cm² = 100 000mm² = 10 dm²
e) A = 1200dm*15m = 120m*15m = 1800 m² = 18 000 000cm² oder gleich in cm umrechnen: 12000cm*1500cm