Corona-Arbeitsaufträge (Bio) LUX

Arbeitsauftrag Biologie8

• Heute nur eine sehr kurze Einheit.
• Ihr könnt die Aufgabe allerdings erst bearbeiten, wenn wir wirklich den vorangegangenen Arbeitsauftrag erledigt habt.
• Vergesst nicht, die Hausaufgabe vom letzten Mal (die ihr auch über den Schulmanager bekommen habt) mir bis Dienstag, 05.05. zu schicken. Danke!

Ein Diagramm

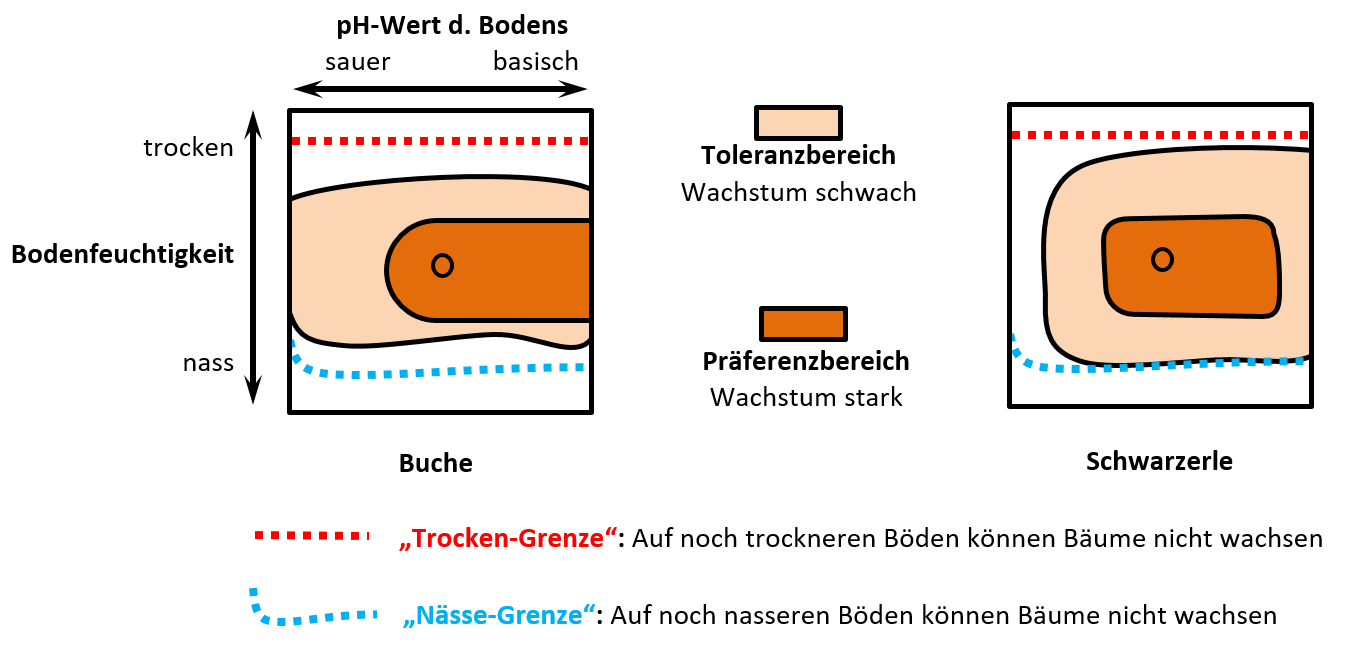
Das folgende Diagramm wurde erstellt, indem man sehr viele Buchen und Schwarzerlen im Freiland untersucht hat. Man hat beurteilt, wie gut diese Bäume wachsen und das in zwei Kategorien eingeteilt: Schwaches Wachstum und starkes Wachstum. Gleichzeitig hat man den Boden untersucht, auf dem die jeweiligen Bäume wachsen: Es wurde die Bodenfeuchte und der pH-Wert gemessen. (Falls ihr das aus der Chemie nicht mehr wisst: Der pH-Wert ist ein Maß dafür, wie sauer oder basisch etwas ist).

• Beschreibt das folgende Diagramm!
• Eine Interpretation ist nicht nötig!
• Beachtet, dass drei Parameter dargestellt sind!
• Erinnert euch an die Begriff, die man für Lebewesen verwendet, die bezüglich eines Umweltfaktors entweder sehr tolerant oder sehr empfindlich sind. Versucht diese Begriff hier mit unterzubringen!

Die Grafik zeigt die Vitalität von Buchen und Schwarzerlen, gemessen als Stärke des Wachstums, in Abhängigkeit vom pH-Wert und der Bodenfeuchtigkeit.
Man erkennt: Beide Bäume besitzen ihr Optimum bei mittleren pH-Werten und mittleren Bodenfeuchtigkeitswerten. Entfernt man sich von diesen Werten, nimmt die Stärke des Wachstums ab.
Die Buche ist ein Generalist (euryök) bezüglich des Parameters pH-Wert (euryacid), während die Schwarzerle auf sehr sauren Böden nicht mehr vorkommt.
Bezüglich der Bodenfeuchtigkeit ist die Buche etwas stärker auf mittlere Feuchtigkeitswerte spezialisiert, während sich die Schwarzerle hier eher generalistisch verhält.

Arbeitsauftrag Biologie7 (verpflichtend)

• Die folgende verpflichtende Unterrichtseinheit hat eine Bearbeitungszeit von ca. 30 Minuten.
• Ihr benötigt für die Bearbeitung: Das Schulbuch, einen Zettel, Stift und Ruhe.
• Bitte bearbeitet die gestellten Aufgaben tatsächlich erst selbst, bevor ihr auf "Lösung" klickt!

Ziel

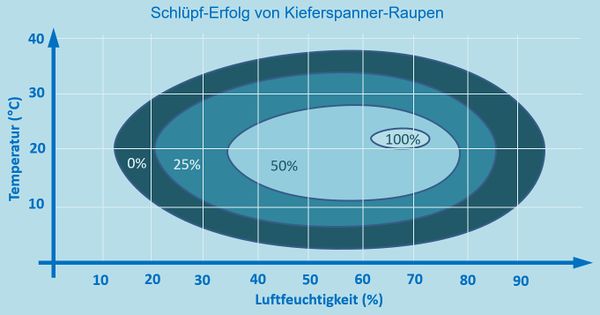
Langfristig möchte ich mit euch den Begriff "ökologische Nische" klären. In dieser Einheit wird das aber noch nicht geschehen. Um diesen Begriff zu verdeutlichen, werde ich bestimmten Grafiken arbeiten. Grafiken, die etwas komplizierter sind, als ihr gewohnt seid.
Eine Grafik, die so ähnlich auch in eurem Buch auf der S. 71 enthalten ist, seht ihr hier:

Wiederholung

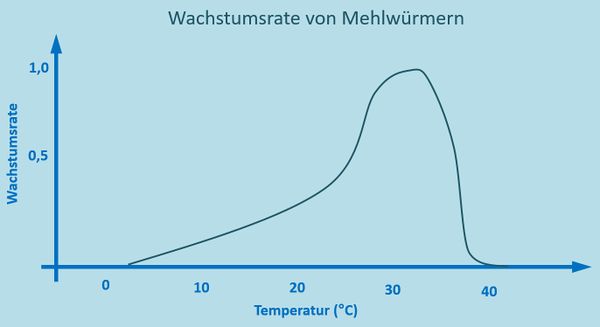
Normalerweise beginnt ihr beim Interpretieren einer Grafik zunächst mit einer bestimmten Floskel: "Die Grafik zeigt... in Abhängigkeit von...". Das funktioniert bei der oberen Grafik nicht! Zur Wiederholung noch einmal anhand einer einfacheren Grafik. Wendet die Floskel an:

• Die Grafik zeigt die Wachstumsrate von Mehlwürmern in Abhängigkeit von der Temperatur.
• Man erkennt eine typische Optimuskurve mit einer optimalen Wachstumsrate bei ca. 30%...
• usw...

Zerlegung der Grafik in Komponenten

Die Floskel kann auf die eingangs gezeigte Grafik nicht angewendet werden, weil hier DREI Parameter dargestellt sind, während die Grafik von den Mehlwürmern nur ZWEI Parameter enthält.

• Mehlwurmkurve: Temperatur, Wachstumsrate
• Kiefernspinner: Temperatur, Luftfeuchtigkeit, Schlüpferfolg

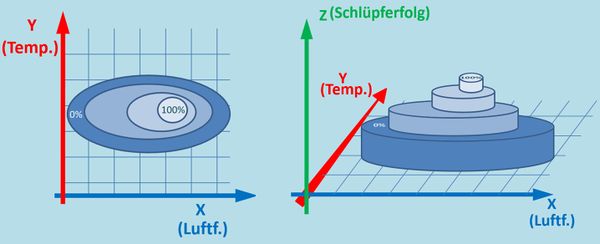
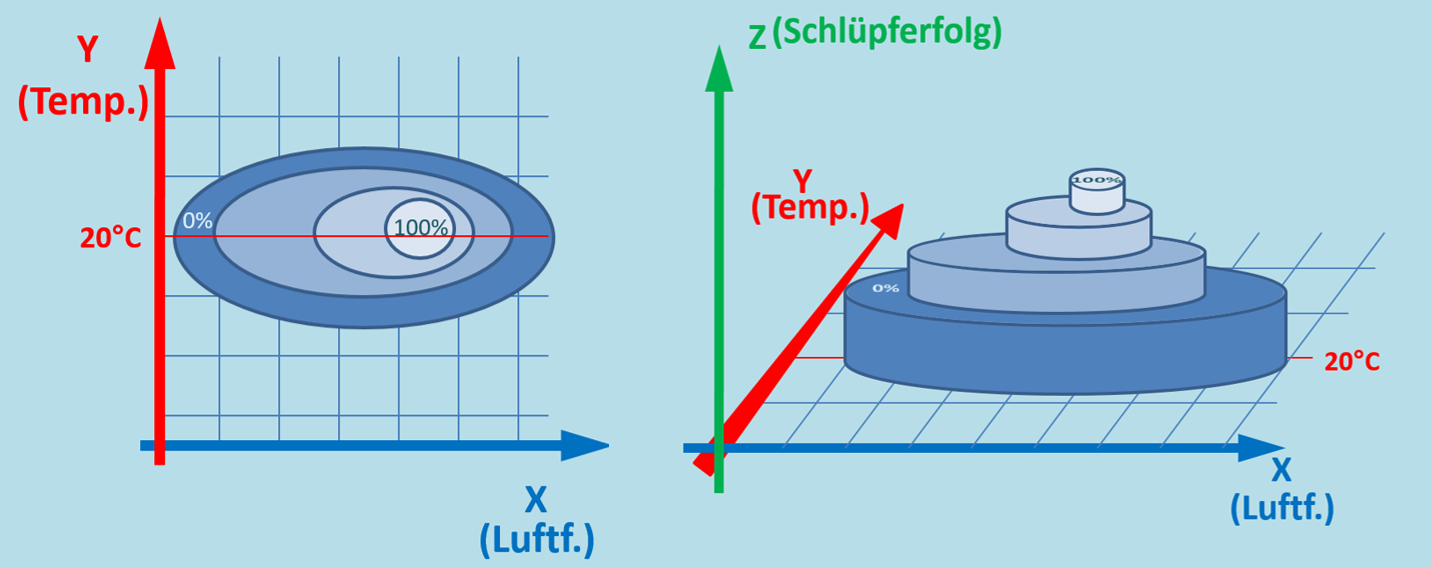
Normalerweise braucht man für jeden Parameter eine eigene Achse. Im Bild vom Kiefernspinner ist die dritte Achse einfach weggelassen, bzw. kommt sie auf euch zu! Das folgende Bild zeigt, wie man sich die Grafik dreidimensional auch vorstellen könnte:


Vielleicht kennt ihr solche Darstellungen aus eurem Atlas: Auch da werden Berge mit "Höhenlinien" dargestellt. Man kann aus der aufgeschlagenen Seite eines Atlas ja kein Gebirge herauswachsen lassen.
Mit dieser Darstellung solltet ihr jetzt auch etwas besser die Floskel anwenden können: Das was in einer zweidimensionalen Grafik die y-Achse ist, ist hier die z-Achse. Und das was in einer zweidimensionalen Grafik die x-Achse ist, ist hier die x- und die y-Achse. Versucht es jetzt mit der Floskel!

Die Grafik zeigt den Schlüpferfolg von Kieferspannern in Abhängigkeit von der Temperatur und der Luftfeuchtigkeit.
Wenn ihr das hinbekommen habt: TOLL! :)

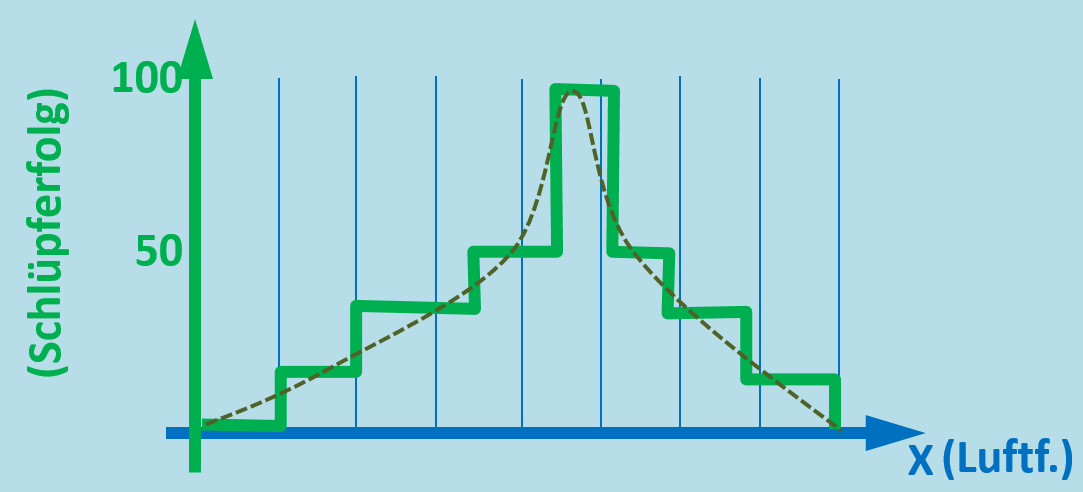
Man kann aus dieser dreidimensionalen Darstellung auch wieder zweidimensionale Grafiken machen, indem man einen Paramater einfach konstant lässt. Zum Beispiel: Man kann den Schlüpferfolg von Kieferspannern in Abhängigkeit von der Luftfeuchtigkeit in eine Grafik zeichnen. Die Temperatur soll in allen Fällen immer gleich bei 20°C bleiben. Versucht diese Grafik zu zeichnen. Dazu ist in der folgenden dreidimensionalen Abbildung eine Hilfslinie hervorgehoben (die rote 20°C-Linie):

• Zeichnet zunächst ein Achsensystem (y-Achse: Schlüpferfolg, x-Achse: Luftfeuchtigkeit)
• Fahrt dann mit eurem Finger die rote Linie auf dem Diagramm hier am Bildschirm entlang und übertragt die Werte, bei denen sich euer Finger gerade befindet in die passende Stelle eures gezeichneten Koordinatenkreuzes.

Die geschrichelte Linie ist eine "geglättete" Linie. Die ist etwas realistischer

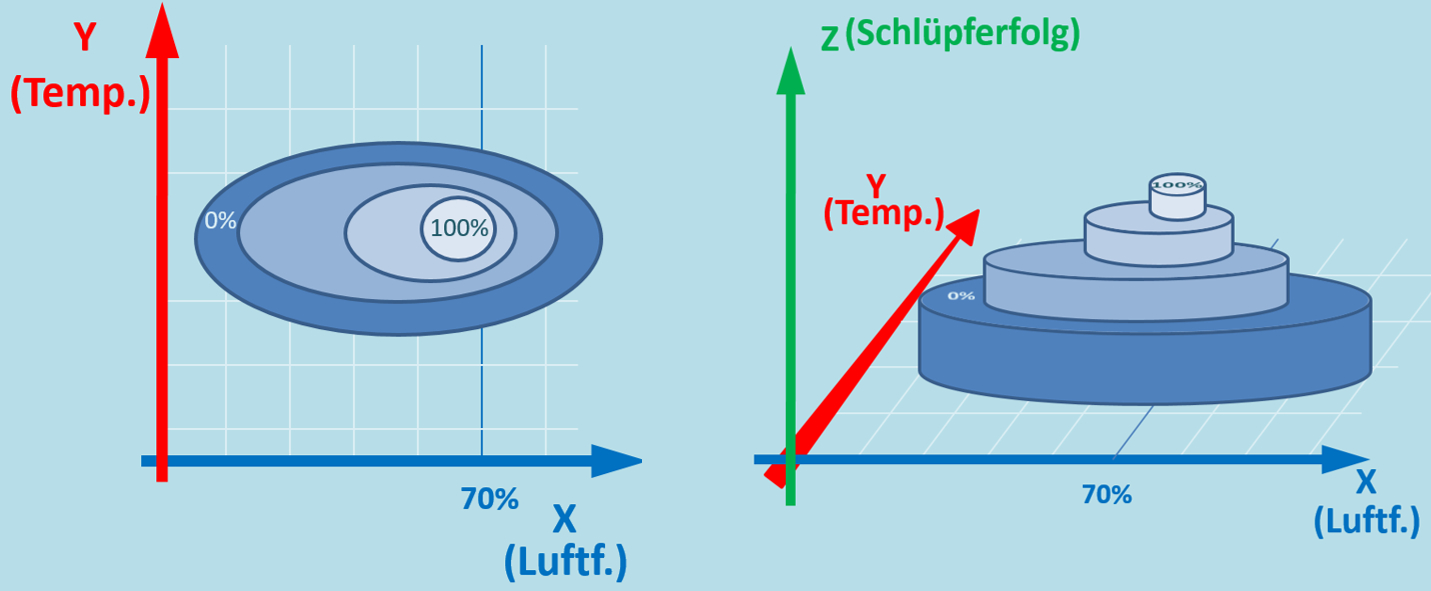
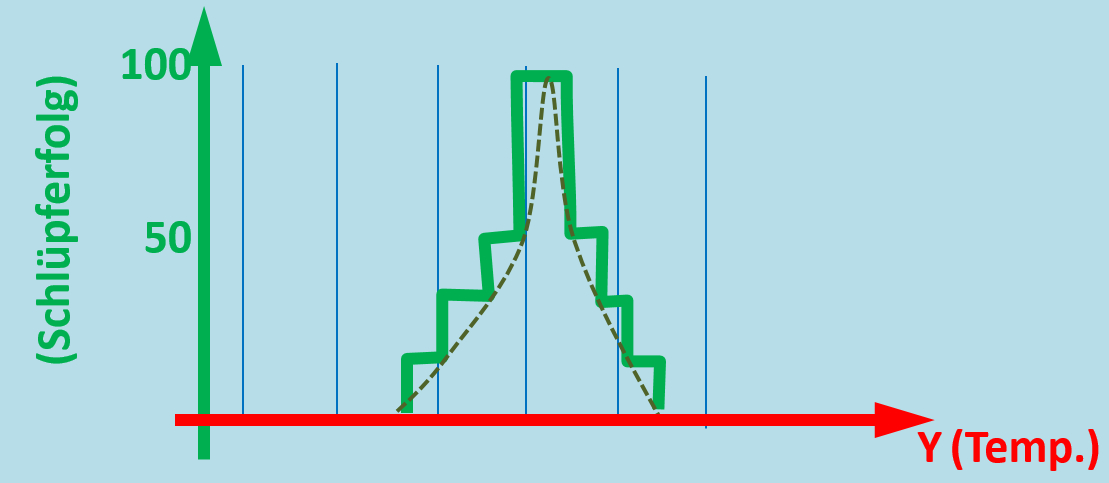
Das Ganze geht natürlich auch mit dem anderen Parameter: Leitet aus dem dreidimenionalen Diagramm ein zweidimensionales Diagramm ab, das den Schlüpferfolg in Abhängigkeit von der Temperatur zeigt. Bei einer gleichbleibenden Luftfeuchtigkeit von 70%. Diesmal ohne Text-Hilfen, nur das entsprechende Diagramm:

Hausaufgabe

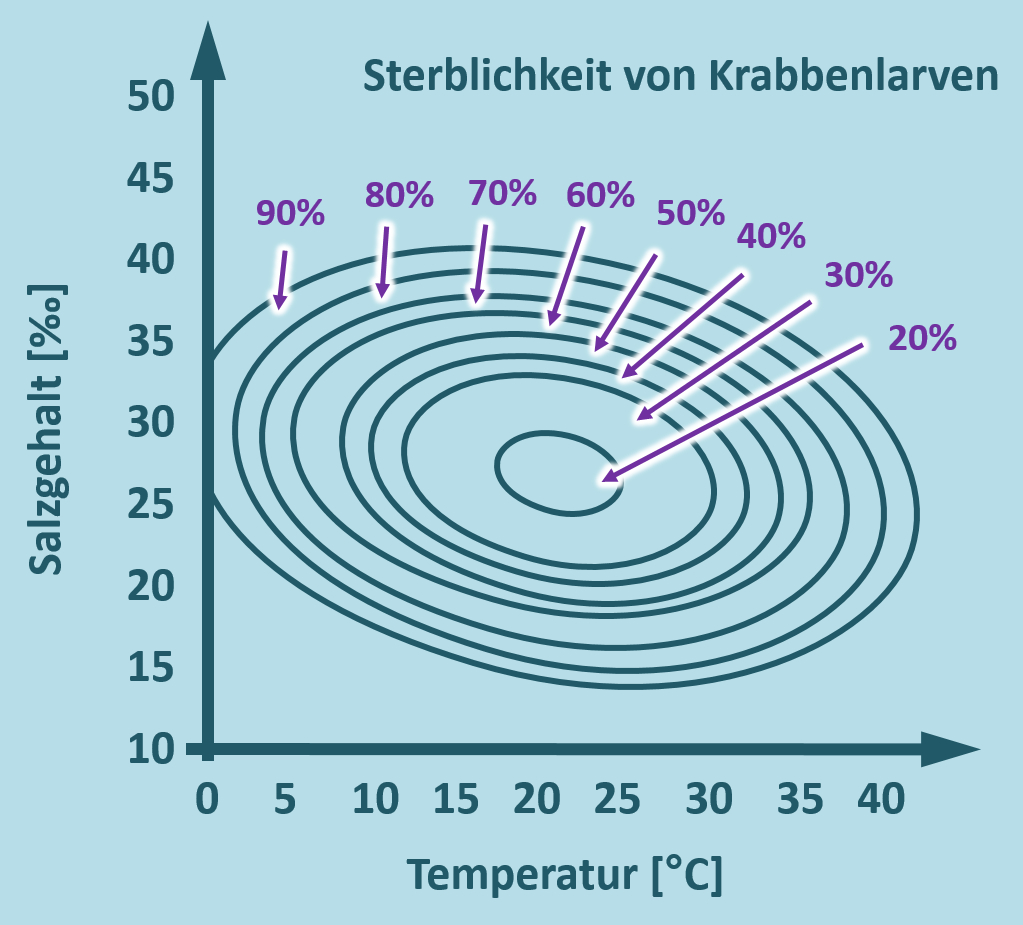
Nach den neuen "Home-Schooling-Regeln" sollen wir Lehrer euch ein ausführlicheres Feedback geben. Daher möchte ich gerne, dass ihr mir die Lösung zu der folgenden Hausaufgabe schriftlich (als Textnachricht) schickt. Das Ganze wird über den Schulmanager laufen, ich kontaktiere euch im Laufe des Tages über den Schulmanager.

• Beschreibt die folgende Grafik!
• Eine Interpretation ist nicht nötig, da ihr die Gründe für den Verlauf nicht kennt.
• Bedenkt aber bitte, dass auch in dieser Grafik DREI Parameter stecken!
  
• Die Hausaufgabe müsst ihr nicht bis morgen erledigen, sondern bis nächste Woche (Di). Morgen kommt allerdings noch eine kleine Einheit dazu.

Arbeitsauftrag Biologie6 (verpflichtend)

• Die folgende verpflichtende Unterrichtseinheit hat eine Bearbeitungszeit von ca. 45 Minuten.
• Ihr benötigt für die Bearbeitung: Das Schulbuch, einen Zettel, Stift und Ruhe.
• Bitte bearbeitet die gestellten Aufgaben tatsächlich erst selbst, bevor ihr auf die Lösung klickt!

Wiederholung

Ihr habt in der letzten Einheit Umweltfaktoren kennengelernt, die einen Einfluss auf Lebewesen haben können.

• Zählt zur Wiederholung fünf solche Faktoren auf!

z.B. Temperatur, Wasserverfügbarkeit, Mineralstoffgehalt, Konkurrenz, Krankheitserreger, Parasiten

Vitalitätskurven

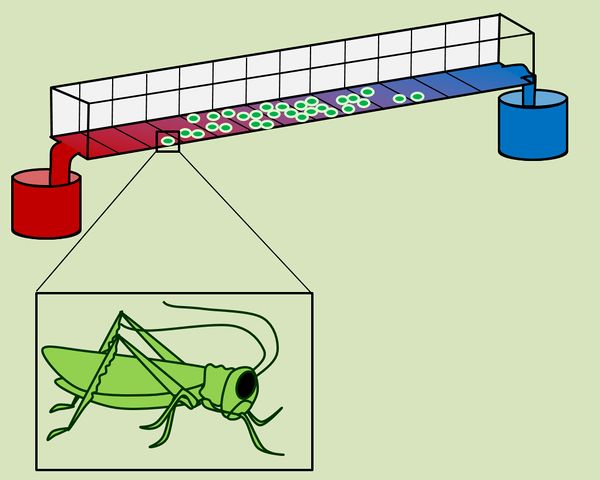
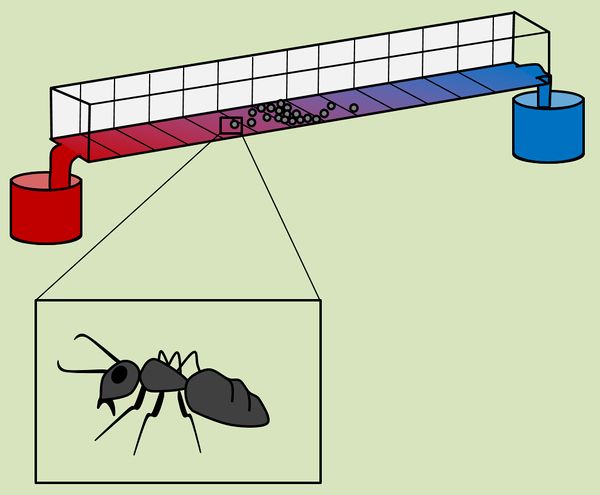
In dieser Einheit sollen die Auswirkungen von zwei abiotischen Faktoren auf Lebewesen etwas genauer unter die Lupe genommen werden. In einem relativ simplen Experiment wurde untersucht, wie die Individuen einer Gruppe auf den Faktor Temperatur reagieren: Eine Metall-Rinne wurde am einen Ende in heißes Wasser, am anderen Ende in Eiswasser getaucht. Da die Wärme vom heißen Wasser sich in Richtung des Eises ausbreitet, entstehen ein Temperatur-Gradient (auch Temperatur-Gefälle oder Temperatur-Orgel genannt). In diese Apparatur kann man kleine Lebewesen setzen, z. B. Heuschrecken und beobachten, wie sie sich verteilen. Das folgende Bild zeigt das Ergebnis:

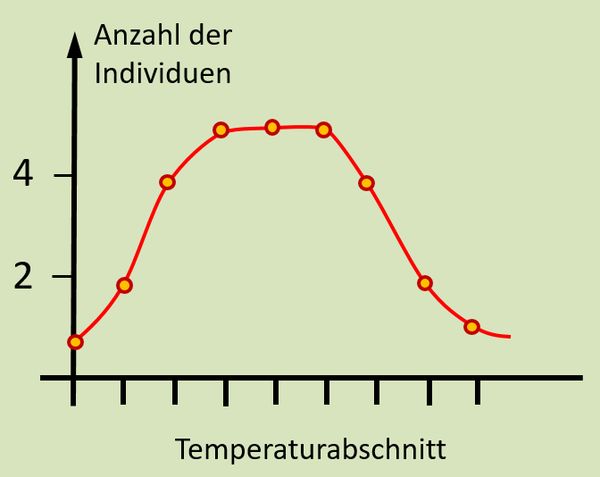
• Beschreibt das Ergebnis zunächst mit Worten!
• Zeichnet dann eine Grafik, die auf der x-Achse die Temperaturabschnitte zeigen soll und auf der y-Achse die Anzahl der Tiere, die sich in den jeweiligen Temperaturabschnitten aufhalten!

• z.B.: Die meisten Tiere bevorzugen eine mittlere Temperatur, nur wenige halten sich in ganz warmen oder ganz kalten Temperaturabschnitten auf

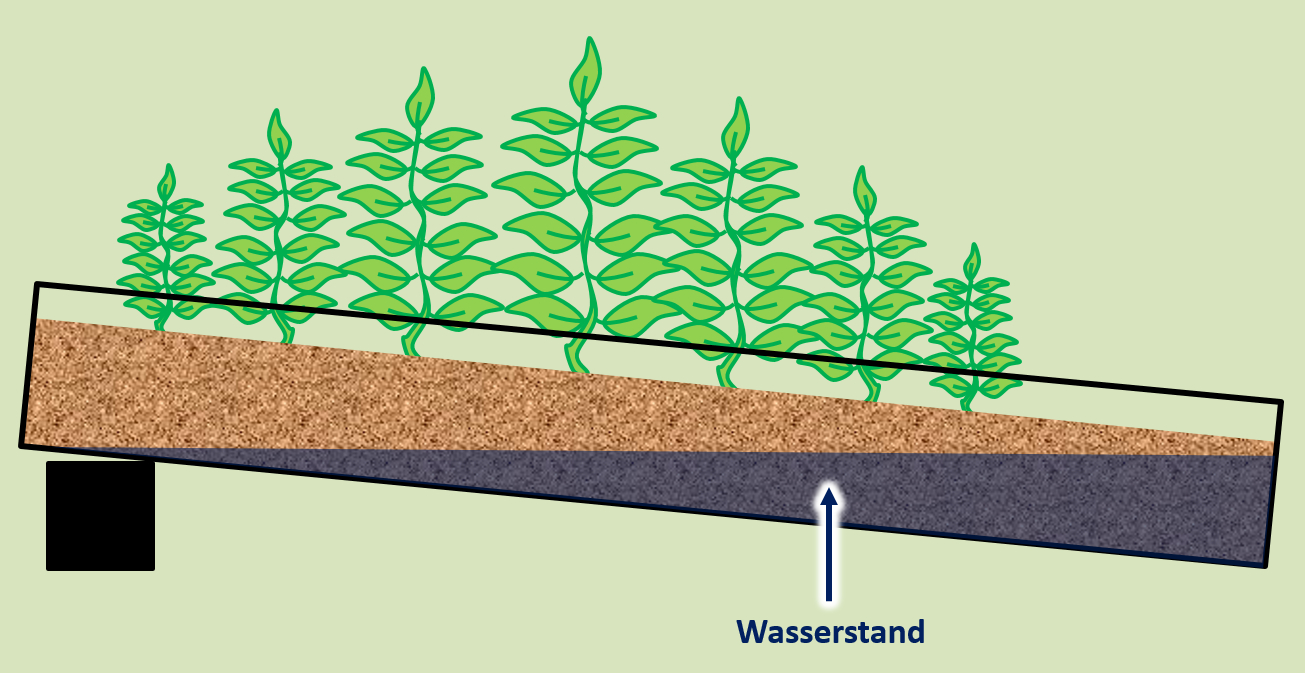
Die sich ergebende Kurve kann allgemein auf andere Umweltfaktoren übertragen werden und man könnte folgende Erklärung formulieren: Die meisten Lebewesen kommen mit einer mittleren Ausprägung eines Faktors (egal ob Temperatur, UV-Einstrahlung, Störgeräusche etc.) am besten klar. Je extremer die Ausprägung eines Merkmals (je heißer, je kälter, je lauter, je intensiver...) desto schwieriger fällt das Überleben.

• Ein anderes Beispiel: Interpretiert die folgende Grafik bei der Pflanzen in einem "Wasserverfügbarkeits-Gradienten" gewachsen sind!

• Die Grafik zeigt das Wachstum von Pflanzen in Abhängigkeit von der Wasserverfübgarkeit. Die Pflanzen wachsen am besten bei mittlerem Wasserstand, sie wachsen deutlich schlechter bei niedrigem oder hohem Wasserstand.

Die beiden Kurven, die ihr jetzt kennengelernt habt sind typisch und gelten allgemein. Ihr könnt das z.B. in eurer Klasse überprüfen: Fragt, wie viele Stunden Schlaf jeder von euch braucht, um sich wohl zu fühlen. Fragt, wie lange ihr gerne im Sommer im Schwimmbad in der Sonne liegt. Fragt, welche Temperatur ihr in eurem Zimmer am angenehmsten empfindet.
Es sollte immer das gleich herauskommen: Die meisten werden einen mittleren Wert bevorzugen, ein paar wenige einen sehr hohen, ein paar wenige einen sehr niedrigen Wert. Man nennt die aus solchen Untersuchungen abgeleiteten Grafiken "Vitaltiätskurven": Auf der y-Achse wird immer eine "Vitalitätsmaß" angegeben. Das kann z.B. sein die Wachstumsrate, die Aufenthaltsdauer, der Ertrag, die Aktivität... immer in Abhängigkeit von der Ausprägung des untersuchten Faktors (z.B. der Temperatur). Der Verlauf entspricht einer "Optimumskurve": Bei einem bestimmten Wert ist die Vitalität "optimal", sowohl "links" als auch "rechts" von diesem Wert fällt die Vitalität ab.
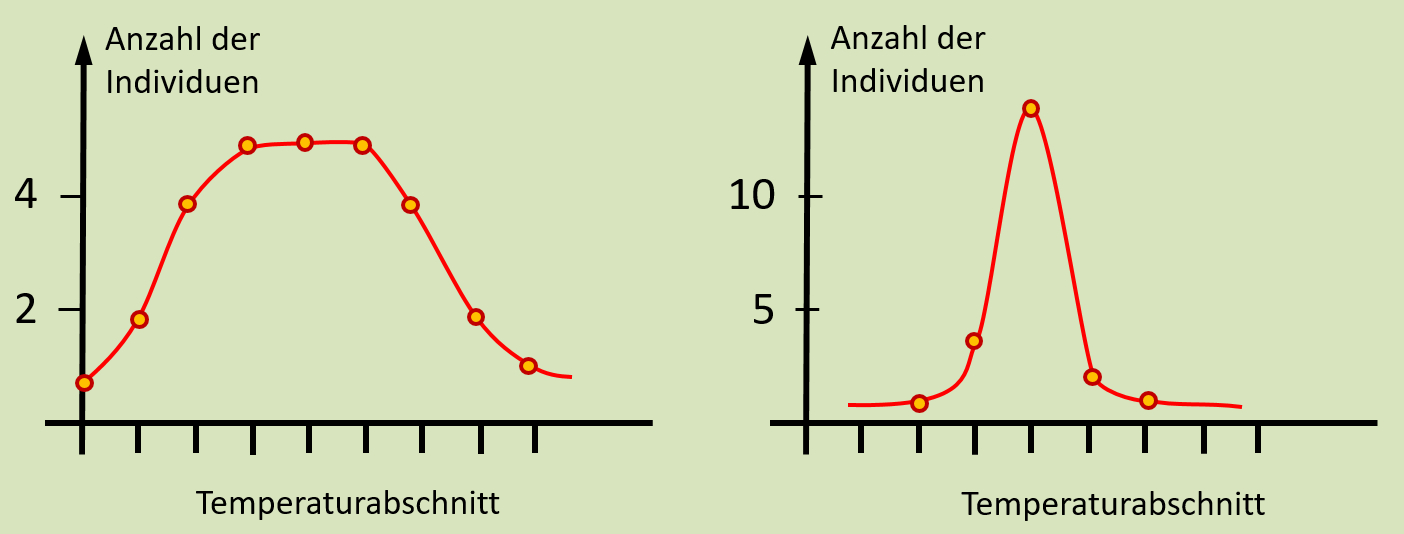
Bei allen Gemeinsamkeiten können sich die Kurven doch leicht unterscheiden. Im ersten hier beschriebenen Versuch mit der Temperatur-Orgel wurden Heuschrecken in die Rinne gesetzt, man kann aber auch Ameisen einer bestimmten Art verwenden. Das Ergebnis zeigt das folgende Bild.

• Zeichnet genau wie beim ersten Versuch eine Grafik, welche die Anzahl der Individuen in den einzelnen Temperaturabschnitten zeigt. Zeichnet die Grafik genau rechts neben die erste (wenn kein Platz mehr auf dem Blatt ist, dann ein neues daneben legen). Versucht die Grafik so zu zeichnen, dass euer höchster y-Wert bei beiden Grafiken ungefähr auf gleicher Höhe liegt.
• Beschreibt den Unterschied der beiden Grafiken!

• Bei der Grafik von den Ameisen halten sich nahezu alle im selben Temperaturbereich auf. Es gibt nur wenige Abweichler und die sind immer noch dicht bei den anderen. Lebewesen, die auf einen sehr engen Bereich bezüglich eines Umweltfaktors begrenzt sind, nennt man Spezialisten, oder als Adjektiv: Sie sind stenök (wenn sie bezüglich vieler Faktoren Spezialisten sind) oder steno... wenn es nur um einen Faktor geht (hier also stenotherm, weil sie Spezialisten bezüglich des Faktors Temperatur sind)
• Bei der Grafik von den Heuschrecken erkennt man, dass sich die Heuschrecken über einen viel größeren Bereich verteilen. Tiere, die Umweltfaktoren in großen Schwankungen tolerieren nennt man Generalisten oder als Adjektiv: Sie sind euryök (wenn sie bezüglich vieler Faktoren Generalisten sind) oder eury... wenn es nur um einen Faktor geht (hier also eurytherm, weil sie Generalisten bezüglich des Faktors Temperatur sind)

Arbeitsauftrag

• Lest jetzt im Buch die S. 70!
• Verinnerlicht vor allen Dingen die Fachbegriffe, die zu bestimmten Teilen einer Vitalitätskurve gehören (Abbildung 2)!
• Bearbeitet dann die Aufgabe 3a auf der Seite 71!

• Die Grafik zeigt die Wachstumsrate von Mehlwürmern in Abhängigkeit von der Temperatur und auch die Anzahl von Mehlwürmern, die sich in einem bestimmten Temperaturbereich aufhalten. Es ergibt sich eine typisch Optimumskurve: Bei ca. 32°C wachsen die Mehlwürmer am besten, hier liegt das Optimum. Sowohl bei niedrigeren also auch höheren Temperaturen geht die Wachstumsrate stark zurück.
• Fachbegriffe für die Buchstaben: A-Toleranzbereich, B-Optimum, C-Pessimum, D(links)-Minimum, D(rechts)-Maximum

Hausaufgabe

Interpretiert auf der S. 70 die Abbildung 1 ausführlich (nur die durchgezogenen Linien, nicht die gestrichelten)!

• Die Grafik zeigt die relative Wachstumsrate der Bachforelle und des Karpfens in Abhängigkeit von der Wassertemperatur. In beiden Fällen liegt eine typische Optimumskurve vor, allerdings liegt bei der Bachforelle das Optimum bei ca. 10°, bei Karpfen ca. bei 20°C. Bei beiden Tieren führt sowohl eine Erhöhung als auch eine Erniedrigung der Temperatur zu einem starken Abfall der Wachstumsrate. Insgesamt ist der Toleranzbereich des Karpfens etwas breiter als der der Bachforelle, insofern könnte man den Karpfen als Generalisten, die Bachforelle als Spezialisten bezeichnen. Man könnte auch sagen, Bachforellen sind stenotherm und Karpfen eurytherm.

Arbeitsauftrag Biologie5 (verpflichtend)

Damit ihr nicht ganze fünf Wochen ohne Biologie-Unterricht gewesen sein, bekommt ihr zum Auffrischen der Thematik in dieser Woche zwei kleine, verpflichtende Unterrichtseinheiten zur Verfügung gestellt.

• Die Einheit sollte ca. 30 Minuten dauern.
• Für die Bearbeitung benötigt ihr: Das Schulbuch, einen Zettel, einen Stift und Ruhe.

Wiederholung

Um wieder in die Thematik hineinzukommen, zunächst eine kleine Wiederholung. In einer der letzten Stunden vor den Ferien wurden Fachbegriffe zum Thema "Ökologie" eingeführt. Im Hefteintrag findet ihr folgendes Bild:

Zu diesem Thema hattet ihr auch schon einmal eine Hausaufgabe auf: Buch S. 63, Aufgabe 1. Wiederholt diese Aufgabe. Dazu müsst ihr auf der linken Seite (S. 62) den blauen "Zettelkasten" lesen. Klickt erst auf "Lösung 1" wenn ihr tatsächlich eine Lösung habt!

Bei dieser Art der Aufgabenstellung macht es Sinn, zunächst die enthaltenen Fachbegriffe (Ökosystem und offen) zu definieren und anschließend die im konkreten Beispiel enthaltenen Elemente den entsprechenden Begriffen zuzuordnen. In diesem Fall also:
Ein Ökosystem setzt sich zusammen aus dem unbelebten Lebensraum, dem Biotop und der Gemeinschaft aller Lebewesen darin, der Biozönose. Ökosysteme sind offene Systeme, das bedeutet, dass sowohl ein Energie- als auch ein Stoffaustausch mit der Umgebung möglich sein muss.
Konkret: Zum Biotop zählen hier das Glas, das Wasser, die Erde (ohne Kleinstlebewesen). Zur Biozönose zählen Bakterien, Kleinstlebewesen (Bärtierchen, Milben), Insekten und Spinnentiere, Moose und evtl. größere Pflanzen. Wenn man noch genauer vorgehen möchte, könnte man nun noch die Begriffe Produzenten (Moose, Pflanzen), Konsumenten ("Tierchen") und Destruenten (Baterien, Pilze) erwähnen.
Das System ist offen. Energie kann in Form von Sonnenlicht und Wäre durch das Glas ins System hinein und heraus. Auch Stoffe können (wenn die Folie entfernt wird) ausgetauscht werden: Wasser, Gase.

Einflussfaktoren auf Lebewesen

Soviel zur Wiederholung der Grundbegriffe. Analysiert nun die folgenden Bildpaare. Auf beiden sind Lebewesen der selben Art zu sehen, die sich jedoch in gewisser Weise unterscheiden. Überlegt, welcher Faktor diese Unterschiede hervorgerufen haben könnte!

• 

  Buchenwald bei Marburg im Winter

• 

  Buchenwald bei Marburg im Frühjahr

Viele Laubbäume werfen im Winter all ihre Blätter gleichzeitig ab. Grund dafür ist die Wasserverfügbarkeit. Aufgrund von Frost steht den Bäumen kein flüssiges Wasser mehr im Boden zur Verfügung. Über die Blätter würde aber weiterhin Wasser verdunsten, was Probleme verursacht. Außerdem würden die Zellen des Blattes beim Gefrieren platzen und das Gewebe wäre zerstört (ähnliches passiert z.B. wenn man eine Erdbeere einfriert. Nach dem Auftauchen ist sie quasi Matsch).

Was könnte hier das unterschiedliche Aussehen hervorgerufen haben? (Zum Vergrößern der Bilder anklicken)

• 

  Kiefern in Kultur. Alle Bäume wurden gleichzeitig dicht an dicht gepflanzt

• 

  Freistehende Kiefer

Die dicht an dicht stehenden Kiefern wachsen alle gleich schnell in die Höhe. Im unteren Bereich lohnt es sich keine Äste mit Nadeln zu erzeugen, weil dort kein Licht hinkommt. Daher sind diese Bäume nur an der Spitze benadelt, während die freistehende Kiefer bis auf den Boden grüne Nadeln erzeugt.

Letzer Vergleich: Welcher Faktor hat hier Einfluss genommen?

• 

  Blätter einer Kastanie

• 

  Blätter einer Kastanie

Das Blatt der Kastanie im rechten Bild ist von einem Parasiten befallen: Einer Miniermotte. Die Raupe dieses kleinen Schmetterlings frisst sich durch die mittleren Schichten des Blattes, das an dieser Stelle dann welkt.

• 

  Larve

• 

  Puppe

• 

  Erwachsene Motte

Die oberen Bilder zeigen drei Beispiele für Faktoren, die ein Lebewesen beeinflussen können. Schreibt diese auf ein Blatt Papier und findet noch fünf weitere! Denkt dabei an Tiere, Pflanzen, Pilze, Einzeller und Bakterien!

• Temperatur, Licht, Parasiten,
• z.B.: Wasserverfügbarkeit (bzw. Feuchtigkeit),
• Mineralstoffgehalt (gedüngter Boden oder nicht),
• Räuber-Beute-Verhältnis (wie viele Feinde gibt es in dem Revier, in dem ein Tier lebt),
• Konkurrenz (wie viele andere Tiere/Pflanzen leben im gleichen Gebiet)
• Krankheitserreger

Diese Parameter kann man in zwei Gruppen einteilen. Macht das und überlegt euch Überbegriffe für beide Gruppen!

Die richtigen Fachbegriffe (biotisch und abiotisch) habt ihr vielleicht nicht gewusst, aber den Unterschied beschreiben konntet ihr wahrscheinlich ganz gut: Die eine Gruppe enthält Faktoren, die mit Lebewesen zusammenhängen (deswegen 'bio'tisch). Die andere Gruppe eher physikalische, chemische Parameter (deswegen abiotisch; die Vorsilbe a bedeutet oft eine Umkehrung des Begriffs: Wenn sich jemand asozial verhält, dann verhält er sich nicht sozial)

Das WW auf dem Doppelpfeil steht für "Wechselwirkungen". Das bedeutet: Ein Parameter der einen Gruppe kann Einfluss haben auf einen Parameter der anderen Gruppe. Überlegt euch zwei solche Fälle und skizziert diese! ("Skizzieren" heißt hier nicht "zeichnen", sondern "mit Worten grob umschreiben".)

• Zum Beispiel: Eine Pflanzen ist von Blattläusen befallen. Wenn es wärmer wird, vermehren sich diese schneller und schaden der Pflanze stärker. Der Faktor Temperatur hat hier Einfluss auf den Faktor Parasit.
• Misteln sind Pflanzen (vielleicht bekannt aus Asterix und Obelix), die auf den Ästen von Bäumen wachsen und dessen Wasserleitungsbahnen anzapfen. Selbst wenn für den Baum genügend Wasser vorhanden wäre, könnte es sein, dass durch die Mistel die Verfügbarkeit knapp wird. Hier hat also der Faktor Parasit einen Einfluss auf den Faktor Wasserverfügbarkeit.

Anwendung an konkretem Beispiel

• Lest nun die Seiten 64 - 65 im Buch!
• Wenn ihr fertig seid, schließt das Buch und legt es beiseite!
• Klickt auf "Fragen anzeigen" und überprüft, ob ihr die Inhalte des Textes anhand der Fragen wiedergeben könnt!
• Lösung 8 sagt euch, ob ihr richtig gelegen habt.

• Das folgende Bild zeigt die Blättchen eines Waldsauerklees. Sie hängen teilweise nach unten, so als ob die Pflanze welken würde. Dies ist jedoch nicht der Fall. Zeige auf, welcher Umweltfaktor dafür verantwortlich ist!
  

• Nenne drei weitere Faktoren, die in der oberen Aufzählung noch nicht vorkommen, für den Sauerklee aber laut Text eine wichtige Rolle spielen! Orden die Faktoren den Begriffen "biotisch" oder "abiotisch" zu.
• Pflanzen scheinen ihren Fressfeinden oft hilflos ausgeliefert zu sein. Das stimmt nicht immer. Es gibt viele Strategien, wie sich Pflanzen vor dem Gefressenwerden schützen können. Beschreibe die Strategie des Sauerklees!
• Erkläre, was man unter dem Begriff "Mykorrhiza" versteht!

• Der Wald-Sauerklee ist sehr empfindlich was Sonneneinstrahlung angeht. Um sich vor einer Überlastung zu schützen klappt der seine Blättchen bei zu starkem Lichteinfall nach unten
• Abiotisch: pH-Wert (wie sauer / alkalisch ist der Boden), mechanische Kräfte, wie z.B. Wind; Biotisch: Symbiose mit Pilzen
• Der Wald-Sauerklee produziert spitze Oxalat-Kristalle. Die erschweren das Fressen der Blätter durch Schnecken oder andere Pflanzenfresser
• Als Mykorrhiza bezeichnet man das Zusammenleben einer Pflanze mit einem Pilz zum gegenseitigen Nutzen (Symbiose). Der Pilz besitzt ein großes Netzwerk an Hyphen, mit denen er Wasser und Mineralstoffe aus einem großen Bereich des Bodens aufnehmen kann. Über eine Verbindung mit dem Pilz können diese Stoffe zum Waldsauerklee gelangen. Umgekehrt liefert der Waldsauerklee organische Stoffe (wie. z.B. Zucker), die der Pilz nicht selbst herstellen kann.

Diese Einheit endet hier. Am Ende der nächsten Einheit wird es einen Hefteintrag geben, den ihr euch hier herunterladen und ins Heft kleben bzw. in eurem Ordner abheften könnt.

Arbeitsauftrag Bio4

Arbeitsauftrag Bio4

Osmose bei Kartoffeln.
Der Prozess der Osmose begegnet euch im Alltag wahrscheinlich häufiger als ihr meint. Auch im Unterricht habt ihr SICHER (!) schon MEHRFACH (!) darüber gesprochen. Für den Fall, dass ihr es trotzdem vergessen haben solltet, hier ein kurzes Video: Hier klicken

Zusammenfassung:
Diffusion: Teilchen verteilen sich freiwillig gleichmäßig im Raum (oder in einem Lösungsmittel). Der umgekehrte Prozess wird nicht beobachtet: Verteilte Teilchen konzentrieren sich nicht an einer Stelle.
Osmose: Existiert eine semi-permeable Membran (dazu zählen auch Zellwände) können bestimmte Teilchen (hier: Wasser) diese passieren, andere nicht (hier: "Salz-Teilchen" oder generell "gelöste Teilchen"). Befinden sich auf der einen Seite der Membran viele gelöste Teilchen, die nicht durch die Membran können, strömen die anderen Teilchen (hier: Wasser) dorthin, um die Konzentration zu verdünnen.

Führt folgenden Versuch durch und macht Fotos von den einzelnen Schritten, damit ihr später ein anschauliches Protokoll erstellen könnt:

• Material: 3 Gläser, Salz, Wasser (am besten destilliertes), Kartoffel
• Schneidet aus einer Kartoffel drei gleich große, längliche Stäbchen (wie Pommes Frites), messt die Länge und legt sie beiseite (es geht auch mit einer Karotte).
• Stellt in den drei Gläsern drei verschieden stark konzentrierte Salzlösungen her:
  • (reines) Wasser: 100g destilliertes Wasser (wenn nicht vorhanden: normales)
  • (physiologische) Kochsalzlösung: 99,1g destilliertes Wasser (wenn nicht vorhanden: normales) + 0,9g Salz (Eine Waage, die 0,9g abwiegen kann hat nicht jeder zu Hause, daher: 0,9g entsprechen ungefähr 2 Messerspitzen. Eine andere Möglichkeit wäre 991g Wasser und 9g Salz zu mischen. Dann habt ihr einen Liter Salzwasser, von dem ihr aber nur ein Glas voll braucht.)
  • stark konzentrierte Kochsalzlösung: 100g destilliertes Wasser (wenn nicht vorhanden: normales) + 1 Teelöffel Salz
• Legt in jede Flüssigkeit einen Kartoffelstreifen
• Wartet 30 - 240 min. (Je nach Dicke der Kartoffel)
• Messt anschließend die Länge der Kartoffelstreifen und biegt die Streifen stark (versucht die beiden Enden zusammenzuführen). Notiert eure Ergebnisse in einer übersichtlichen Tabelle.

Arbeitsauftrag Bio3

Arbeitsauftrag Bio3

Bringt eine Zwiebel zum Keimen!
Sucht euch ein Gefäß (am besten ein durchsichtiges Glas), auf dessen Öffnung sich eine Zwiebel platzieren lässt. Füllt das Gefäß so weit mit Wasser, dass die vertrockneten Wurzeln der Zwiebel eintauchen können. Das untere Bild zeigt, wie es aussehen sollte. Macht jeden Tag ein Foto von diesem Versuchsansatz. Füllt bei Bedarf Wasser nach.
Zusatzaufgabe: Wenn ihr vor eurem Versuchsansatz eine Halterung baut, in der ihr euer Handy / den Fotoapparat einspannen könnt, so dass das Foto jeden Tag aus der exakt selben Perspektive aufgenommen wird, kann man aus den Bildern später eine Zeitraffer-Aufnahme machen. Probiert das! Hinweis: Wenn ihr Wasser nachfüllen müsst, achtet darauf, dass ihr die Zwiebel wieder exakt auf die selbe Position setzt. Sonst wird die Zeitrafferaufnahme nicht schön. Ihr könnt auch einen (dicken) Strohhalm zwischen Glasrand und Zwiebel einklemmen, über den ihr Wasser nachfüllt. Das erfordert alles etwas Geschick, ist aber machbar!

Das Foto zeigt die Entwicklung nach 7 Tagen. Wenn man die Zwiebel nun in einen Topf mit Erde überführt, wird sie grüne Triebe bilden.

Arbeitsauftrag Bio2

Arbeitsauftrag Bio2

Sofern ihr nicht unter häuslicher Quarantäne steht: Findet eine Taubnessel! Pflückt einen Stängel und fertigt zu Hause mit einem scharfen Messer einen Querschnitt davon an. Beschreibe den Querschnitt! Unter Umständen hilft eine Lupe.

Der Stängel ist vierkantig und hohl.

Arbeitsauftrag Bio1

Arbeitsauftrag Bio1

Sucht in eurem Garten oder der näheren Umgebung drei wilde Pflanzen (keine gekauften Zier-Pflanzen in Töpfen etc.), die gerade blühen. Sie sollten in drei verschiedenen Farben blühen. Findet heraus, wie die Pflanzen heißen!

Aktuell blühen z.B.:

• 

  Schneeglöckchen (weiß)

• 

  Winterling (gelb)

• 

  Ehrenpreis (blau)